प्रस्तावनाखंड : विभाग पांचवा- विज्ञानेतिहास.
प्रकरण १३ वें.
गणितशास्त्राचा इतिहास
अपोलोनिअसनंतरचे व अरबांपूर्वींचे गणितज्ञ.- एराटॉस्थिनीझ (ख्रि. पू. २७५-१९४) हा फलज्योतिषी होता. त्यानें द्वित्तघन तयार करण्याचें एक यंत्र तयार केलें व मूलसंख्येचा तक्ता कसा तयार करावयाचा याविषयीं एक नियम प्रसिद्ध केला. याविषयीं पूर्वी माहिती आलीच आहे. (पृ. ३३१ पहा).
हिपसिक्लस हा ख्रिस्तपूर्व दुस-या शतकांत होऊन गेला. यानें युक्लिडचें चौदावें पुस्तक लिहिलें असें म्हणतात.
हिप्पार्कस (ख्रि. पू. १२०) हा प्रसिद्ध ज्योतिषी होता. ह्याची अपचक्राची (एपिसायकल्स) उपपत्ती प्रसिद्ध आहे. ह्यानें त्रिकोणमितीचें नवीन शास्त्र निर्माण केलें व त्रिज्येचा एक तक्ता तयार केला. ह्यानें १२ पुस्तके लिहिलीं होतीं. ती अनुपलब्ध आहेत. या संबंधींहि माहिती पूर्वी आलेलीच आहे (पृ ३३४ पहा).
त्यानंतर हेरॉन म्हणून एक गणिती होऊन गेला. त्याचा कालनिर्णय नक्की झाला नाहीं. ह्याच्या डायोपॅट्रा पुस्तकांत ह्यानें त्रिकोणाचें क्षेत्रफळ काढण्याची रीति दिली आहे.
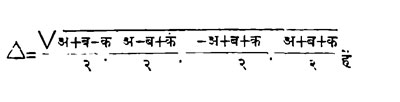 हें सूत्र अजून त्याच्याच नांवानें चालत आहे. ह्यानें आपली बुद्धि निरनिराळ्या प्रकारचीं यंत्रें शोधून काढण्यांत खर्च केली. इजिप्त हें रोमन साम्राज्यांत जसजसें अंतर्गत होत चाललें तसतसा पूर्व व पश्चिम ह्यांचा संगम दृढ होत चालला. ह्या काळांत गणितशास्त्राचा अभ्यास जोरांत सुरू झाला व खालीं दिलेले निरनिराळे गणिती होऊन गेले.
हें सूत्र अजून त्याच्याच नांवानें चालत आहे. ह्यानें आपली बुद्धि निरनिराळ्या प्रकारचीं यंत्रें शोधून काढण्यांत खर्च केली. इजिप्त हें रोमन साम्राज्यांत जसजसें अंतर्गत होत चाललें तसतसा पूर्व व पश्चिम ह्यांचा संगम दृढ होत चालला. ह्या काळांत गणितशास्त्राचा अभ्यास जोरांत सुरू झाला व खालीं दिलेले निरनिराळे गणिती होऊन गेले.
मेनेलॉस ( इ. स. ९८ ) नें त्याच्या नांवानें चालत असलेला सरल भूमितींतला सिद्धांन्त शोधून काढला, व त्याला अनुरूप असलेला सिद्धांत गोलीय भूमितींत सिद्ध करून दाखविला. ह्यानंतर सेरेनस नांवाच्या एका गणित्यानें एक नवीन सिद्धांत सरलभूमितींत शोधून काढला.
इ. स. १३९ च्या सुमारास टॉलेमी हा प्रसिद्ध ज्योतिषी होऊन गेला. त्यानें अल्माजेस्ट नांवाचें एक पुस्तक लिहिलें. त्यानें वर्तुळाचे ३६० भाग करून, त्या प्रत्येकाचे ६० व पुन्हा त्या प्रत्येकाचे ६० असे भाग केले व गणिताचें काम बरेंच सोपें केलें. ह्यानेंहि हिप्पार्कसप्रमाणें त्रिज्यांचा एक तक्ता तयार केला. सरल भूमितींत त्याच्या नांवानें प्रसिद्ध असलेला सिद्धांत त्यानें शोधून काढला. समांतर रेषा गृहीतकृत्य सिद्ध करण्याचा त्यानें प्रयत्न केला पण त्यांत त्याला यश आलें नाहीं. त्रिकोणमितीचें शास्त्र त्यानें बरेंच पूर्णत्वास नेलें याबद्दलची माहिती ज्योति:शास्त्रांत पूर्वी आली आहे (पृ. ३३७ पहा).
पॅपस (इ. स. ३००-७००) यानें पुष्कळ ग्रंथ लिहिले. पण त्यांपैकीं उदाहरणसमुच्चय नांवाचा एकच ग्रंथ अपूर्ण स्थितींत हयात आहे. त्यांत त्यानें उपलब्ध असलेल्या गणितज्ञानाचें पृथक्करण रीतीनें सार काढलें आहे, व त्यामुळें गणिताच्या प्रगतीला बरीच मदत झाली आहे. ह्यांतील बरीच माहिती विश्वसनीय आहे. ह्या पुस्तकांत पॅपसनें स्वत: शोधून काढलेले कांहीं सिद्धांत आहेत, ते अद्याप त्याच्या नांवानें चालत आहेत.
ह्यानंतर थीऑननें ( इ. स. ३७० ) युक्लिड व अल्माजेस्ट या ग्रंथांवर ऐतिहासिक टिपणासहित टीका लिहिल्या; त्या फारच उपयुक्त आहेत. ह्याची मुलगी हिपॉटिआ एक विदुषी व प्रसिद्ध अध्यापिका होती.
विशदता, निश्चित कल्पना व युक्तिवाद करतांना दिसून येणारी सूक्ष्म बुद्धि हे ग्रीक लोकांचे गुण कोणासहि आश्चर्यचकित करून टाकतात. त्यांच्या कालच्या दृष्टीनें त्यांचे दोष पाहूं जातां ते जवळ जवळ दिसतच नाहींत. त्यांनां ऋण व धन राशी रेशांनीं दाखवितां येत नसल्यामुळें सर्वसाधारण सिद्धांत देतां आले नाहींत.
रोमन लोक युद्धकलेंत व राज्यकलेंत अतिश्रेष्ठ होते, पण तत्त्वज्ञान, काव्य वगैरे गोष्टींत ते ग्रीक लोकांची नक्कल करीत असत. पण गणितांत त्यांनीं एवढेंहि केलें नाहीं. मग प्रगतीची गोष्ट तर दूरच.
अरब लोकांचें गणितज्ञान
महमुद मक्केहून मदिनेस गेल्यानंतर सुमारें १२० वर्षांनीं बगदाद येथें हिंदूंच्या शास्त्रांच्या अध्ययनास सुरुवात झाली. ( ८१३-८३३ ) ह्या काळीं महमुद इबन मुसा अलख्वारिझमी ह्यानें एक अंकगणित लिहिलें. ह्यांत हिंदूंची अगाध कल्पकता ग्रंथकर्त्यानें उत्तम रीतीनें दाखविली आहे. कालांतरानें अरबलोकांच्या वरचें हिंदूंचें बौद्धिक वर्चस्व जाऊन त्या ऐवजीं ग्रीक लोकांचे बसूं लागलें. ह्याच गृहस्थानें एक बीजगणित लिहिलें. त्याचें नाव अलशब्रवल मुकाब्ल असें होतें ह्यावरूनच या शास्त्रास अलजिब्रा असें नांव पडलें. ह्यांत हिंदूंच्या व ग्रीकलोकांच्या ज्ञानाची खिचडी आहे. अरबलोकांनी वर्गात्मक व घनात्मक समीकरणें भूमितीच्या पद्धतीनें कशी सोडवावयाचीं हें दाखविलें आहे. घनात्मक समीकरणांची मूळें परस्परांस छेदणा-या शंकुच्छेदांच्या सहाय्यानें त्यांनी काढून दाखविली. अलक्युरेशीनें खालील श्रेढी त्यांच्या बेरजांसकट दिल्या आहेत.
१२ + २२ + ३२ -- + न = २ ब + १/३ (१ + २ + ३ -- + न)
१३ + २३ + ३३ -- + न३ = (१ + २ + ३ -- + न )२
इ. स. ६४० मध्यें अलेक्झांड्रिया उध्वस्त झाल्यानंतर पूर्वेकडें ग्रीक लोकांची विद्या अरबलोकांनीं संभाळून ठेविली. त्यांनीं ग्रीक पुस्तकांची आपल्या भाषेंत भाशांतरें करण्यापलीकडे विशेष कांहीं केलें नाहीं. अलख्वारिझमीनें भूमितीवर जें कांहीं थोडें बहुत लिहिलें आहे त्यावरून त्याजवर असलेला ग्रीक भूमितीचा पगडा दिसून येतो. अरब लोकांनीं त्रिकोणमितीचा अभ्यास बराच केला व घनात्मक समीकरण भूमितीच्या पद्धतीनें कसें सोडवावयाचें हें दाखविलें. गोलीय त्रिकोणमितींत त्यांनीं कांहीं सूत्रें नवीन बसविलीं. अलबाटेग्निअसनें ज्याङ / कोटिज्याङ = द ह्यावरून ज्याङ = 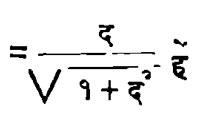 काढून ङ ची किंमत काढलीं. हें ग्रीक लोकांनां यापूर्वी माहित नव्हतें त्याचप्रमाणें कोटिज्याअ = कोटिज्याब. कोटिज्याक + ज्याब.ज्याक.कोटिज्याअ हेंहि सूत्र त्यानेंच बसविलें. अबुल वाफानें ज्यांचा एक तक्ता तयार करून त्यांत अर्ध्या अंशाच्या ज्यांची सुद्धां दशांशाच्या ९ स्थलांपर्यंत किंमत दिली आहे. त्यानेंच स्पर्शज्या हें फल नवीन प्रचारांत आणलें व त्याचा तक्ता तयार केला. त्यानंतर नासिर एदिन ह्यानें त्रिकोणमितींत इतकी प्रगति केली कीं, यूरोपमधील कांही लोकांनां हे अरब लोकांचे शोध माहित होते व ते त्यांनी आपलेच म्हणून प्रसिद्ध केले असें कांहीं लोकांचे म्हणणें आहे.
काढून ङ ची किंमत काढलीं. हें ग्रीक लोकांनां यापूर्वी माहित नव्हतें त्याचप्रमाणें कोटिज्याअ = कोटिज्याब. कोटिज्याक + ज्याब.ज्याक.कोटिज्याअ हेंहि सूत्र त्यानेंच बसविलें. अबुल वाफानें ज्यांचा एक तक्ता तयार करून त्यांत अर्ध्या अंशाच्या ज्यांची सुद्धां दशांशाच्या ९ स्थलांपर्यंत किंमत दिली आहे. त्यानेंच स्पर्शज्या हें फल नवीन प्रचारांत आणलें व त्याचा तक्ता तयार केला. त्यानंतर नासिर एदिन ह्यानें त्रिकोणमितींत इतकी प्रगति केली कीं, यूरोपमधील कांही लोकांनां हे अरब लोकांचे शोध माहित होते व ते त्यांनी आपलेच म्हणून प्रसिद्ध केले असें कांहीं लोकांचे म्हणणें आहे.
स्तिमित व मध्ययुगांतील पाश्चात्य गणितज्ञान.

