प्रस्तावनाखंड : विभाग पांचवा- विज्ञानेतिहास.
प्रकरण ३ रें.
प्राथमिक ज्ञानाची उत्पत्ति-संख्यालेखन.
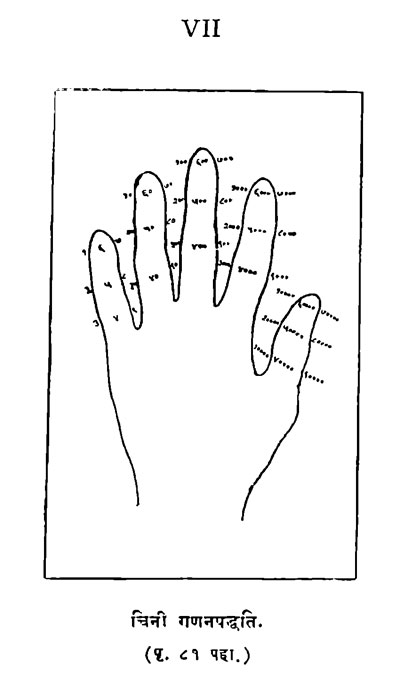तीनपर्यंत मोजण्याची शक्ति:- ‘ संस्कृत भाषेचा उलगडा ’ या आपल्या ग्रंथांत रा. विश्वनाथपंत राजवाडे म्हणतात कीं, संस्कृतामध्यें एकवचन, द्विवचन व बहुवचन हीं तीन वचनें व त्यांस असलेले प्रत्यय हे प्राचीन काळीं आपल्या पूर्वजांनां केवळ तीनच आंकडे मोजतां येत होते अशा परिस्थितीची स्मारकें आहेत. अंदमानांतील कांही जातींनां ३ पलीकडे मोजतां येत नाही; व असें मानण्यास जागा आहे कीं, आज जे सुधारणेच्या शिखरास गेलेले आहेत त्यांचे पूर्वज एके काळी अंदमानांतील वर सांगितलेल्या लोकांइतकेच हिशेब करण्यांत कुशल असत. आपल्या बोटांना प्रत्येकीं तीन पेरीं आहेत यावरून तीनच्या गटांनी हिशेब करण्याची पद्धति सुचली असावी; अंगठा सोडून चार बोटांवर हिशेब करणारांनी चतुर्मानपद्धति काढली; चार बोटें व त्या प्रत्येकाची तीन पेरीं या सर्वांचा उपयोग करणें ज्यांनां सुचलें त्यांनी द्वादशमान पद्धति उदयास आणली; एका हाताच्या सर्व बोटांचा उपयोग करणारांना पंचमानपद्धति सुचली व दोन्ही हातांच्या बोटांचा एकदम उपयोग करणार्‍यांनां दशमानपद्धति सुचली; इत्यादि तर्क करणें धाडसाचें आहे असें बेली साहेबांनां वाटत नाहीं. हिशेब करण्याकडे हाताचा उपयोग करण्याची वहिवाट फार प्राचीन व सार्वत्रिक असल्याबद्दलचा पुरावा पुष्कळ मिळतो. इजिप्शियन चित्रलिपीत लांबीचीं मापें हात व हाताचीं बोटें यांच्या चित्रांनींच दाखवीत. तुरेनियन जातीच्या पुष्कळ भाषांत ‘ अनामिका ’ अशा अर्थांचें नांव संस्कृत अनामिक शब्दानें दाखविल्या जाणार्‍या बोटाला दिलेलें आढळतें. विवक्षित बोटालाच ‘ अनामिका ’ नांव कां पडलें हें सांगणें जरी कठिण आहे तरी असें असण्याचा संभव आहें कीं, हिंदूंच्या व जुन्या अंकपाठांत नऊ अंकाचे गट असल्यामुळें नऊ अंक मोजण्याला जरूर अशा नऊ बोटांचा उपयोग हिशेबांत करून जें एक बोटे मोकळें सोडीत त्याला अनामिका हें नांव पडलें असावें. अशा तर्‍हेच्या स्पष्टीकरणास अडचण अशी कीं, नऊ अंक मोजून स्वाभाविकपणें वगळलें जाणारें बोट करंगळीजवळचें असूं शकणार नाहीं. एकतर करंगळी शिल्लक राहिल, किंवा अंगठा शिल्लक राहील, असो. अनामिका शब्दाची उपपत्ति जरी सोडून दिली तरी बोटे व मोजणें यांचा संबंध निकट आहे हें खास. चिनी लोक एका हाताच्या पांच बोटांचा उपयोग करून ९९,९९९ पर्यंत हिशेब करतात. ही हिशेब करण्याची रीत अशी आहे कीं, करंगळीवर ९ पर्यंत मोजावयाचे; १० ते ९० अनामिकेवर, १०० ते ९०० मधल्या बोटावर, १००० ते ९००० तर्जनीवर व १०,००० ते ९०,००० अंगठ्यावर. पुढें उलट क्रमानें करंगळी पर्यंत आलें म्हणजे ९९,९९९ होतात. पाठ व दोन बाजू यांच्या योगांने चिनी लोक प्रत्येक बोटाच्या तीन बाजू कल्पून बोटाच्या पेर्‍यांनी या प्रत्येक बाजूचे पुन्हां तीन भाग करतात, व ह्या नऊ भागांचा १ ते ९,१० ते ९० वगैरे संख्या दाखविण्याकडे उपयोग करतात. मोजावयास आरंभ करंगळीच्या बाहेरच्या बाजूकडून वरच्या पेर्‍यापासून व शेवट करंगळीच्या आंतल्या बाजूस खालच्या पेर्‍यांत करून यांच क्रमानें पुढें १० ते ९०, १०० ते ९०० वगैरे इतर बोटांवर मोजण्याची त्यांची वहिवाट आहे. हिंदुस्थानांतील व्यापारी लोक आपसांमध्यें जिनसांचे भाव ठरवितात ते एकमेकांचे हात पांघरूणाखाली धरून व परस्परांच्या हातांवर बोटांनी संकेत करून ठरवितात हें प्रसिद्ध आहे. बीड नांवाचा प्राचीन इंग्रज इतिहासकार अशाच प्रकारच्या हिशेबाच्या कामीं बोटांचा उपयोग करण्याच्या तत्कालीन पद्धतीसंबंधानें लिहितांना ती फार पुरातन काळापासून चालत आली आहे असें म्हणतो. ख्रिस्ती शकाच्या आठव्या शतकांतल्या स्मर्ना येथील निकेलस र्‍हाब्डा यानें ज्या पद्धतींचें वर्णन केलें आहे तिनें दहा हजारांच्या खालच्या सर्व संख्या दोन्ही हातांच्या बोटांवर व्यक्त करतां येत होत्या. ह्या पद्धतीमध्यें डावा तळहात उघडा करून त्याची करंगळी, अनामिका व मध्यमा यांपैकीं एक किंवा अधिक बोंटें ताठ ठेवून, अर्धी मिटून किंवा पूर्ण मिटून नऊपर्यंत अंक मोजीत असत. राहिलेल्या दोन बोटांनां निरनिराळ्या स्थितींत ठेवून त्यांचा दहापासून नव्वदपर्यंत दशकाचे नऊ अंक दाखविण्याकडे उपयोग करीत. उदाहरणार्थ, अंगठा व तर्जनी यांची टोंकें एकमेंकांस लावून तीं बोटें ताठ केलीं कीं तीस व अंगठा वाकवून त्याच्या पुढच्या पेर्‍याच्या पाठीजवळ तर्जनींचें टोंक आणलें कीं पन्नास व्यक्त केले जात. उजव्या हाताच्या याच बोटांचा शतकांचे नऊ अंक दाखविण्यासाठीं अशाच रीतीनें उपयोग केला जाई; व उजव्या हातावर एकंच्या अंकाच्या खुणा केल्या असतां सहस्राचे अंक व्यक्त होत. हिशेबाच्या कामीं हाताचा उपयोग करण्याची वहिवाट येणेंप्रमाणें फार पुरातन असल्याने दशमानादि सर्व गणनपद्धती त्यांच्या रचनाकारांनां हातावरूनच सुचल्या असाव्या असें मानण्यास बराच आधार आहे. तथापि इजिप्शियन लोकांत जी पंचमानपद्धति प्रचलित होती ती त्या वेळीं माहीत असलेल्या पांच ग्रहांच्या ग्रहमालेवरून त्यांनां सुचली असावी हा व असल्याच प्रकारचे दुसरे जे कांही तर्क संशोधकांनीं केले आहेत तेहि खरे असण्याचा संभव आहे असें बेली साहेबांनां वाटतें.
